We bouwen een … (2)

Vorige keer zagen we wat je allemaal kunt doen met vierkanten en rechthoeken. Vandaag breid ik dat uit met drie- of meerhoeken en cirkels.

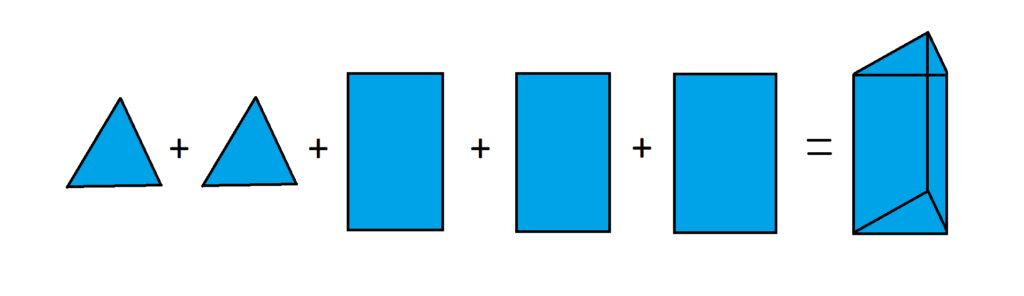
Als je kijkt naar het dak van de meeste huizen of het tentje waarin je kampeert, dan heeft dat de vorm van een prisma. Wanneer onze set bouwsteentjes naast rechthoeken ook twee precies gelijke driehoeken bevat kun je zo’n prisma proberen te bouwen. Niet alleen driehoeken, maar ook rechthoeken heb je nodig, precies evenveel als het aantal zijden van een driehoek. Dat zijn er dus drie. Ook moet je ervoor zorgen dat de lengte van de rechthoeken even groot is en dat de breedte gelijk is aan de zijde van de driehoek waar je hem aan wilt monteren. In het plaatje hierboven heb ik expres een iets bredere rechthoek gezet, omdat een van de zijden van de driehoek ook iets langer is.

Wat je nu gebouwd hebt is een eenvoudig prisma met twee dezelfde driehoeken en drie rechthoeken. Je noemt dat ook wel een driehoeksprisma, maar dat hoef je niet te onthouden. Heb je geen driehoeken, maar twee precies gelijke vijfhoeken, dan werkt het precies zo, maar heb je natuurlijk vijf rechthoeken nodig, een voor iedere zijde, en dat noemen we dan een vijfhoeksprisma.

Een prisma heeft altijd twee grondvlakken, de afspraak onder wiskundigen is dat de rechthoeken geen grondvlak zijn (al zou het wel kunnen). Wat geen grondvlak heet noemen we zijvlak. Verder zijn er twee keer zoveel hoekpunten als het aantal hoeken van je grondvlak. Bouw je met driehoeken, dan krijg je zes hoekpunten, met vijfhoeken zijn het er 10. Het aantal ribben is drie keer zo groot als als het aantal punten van het grondvlak. Heb je een zeshoekig grondvlak, dan heb je 18 ribben.

Het aantal hoeken van het grondvlak maakt dus niets uit bij een prisma. Wat zou er echter gebeuren als het aantal hoeken oneindig groot wordt? Probeer maar eens een twintighoek te tekenen. Als je die uitknipt, dan kun die al bijna rollen. Hoe groter het aantal hoeken, hoe makkelijker dat rollen gaat. Met andere woorden, het gaat steeds meer op een cirkel lijken. En wanneer je twee gelijke cirkels hebt kun je een cilinder bouwen. Je hebt dan niet oneindig veel rechthoekjes nodig, maar gewoon 1, waarvan een van de zijdes gelijk is aan de omtrek van de cirkel. Is de cilinder af, dan heb je twee grondvlakken en een gebogen zijvlak.

Nu gooien we de meeste rechthoeken weg. We houden er nog eentje over, bijvoorbeeld een vierkant. Met een vierkant als enig grondvlak en vier driehoeken kun je weer een ander figuur bouwen de piramide. Er moeten altijd evenveel driehoeken zijn als het aantal zijden van het grondvlak. Net als bij de prisma moet er één zijde zijn die precies even lang is als de zijde van het grondvlak waarop je hem monteert. Daarnaast moeten de andere zijden van de driehoek even lang zijn en ook moeten de driehoeken even hoog zijn. Alleen dan kun je het voor elkaar krijgen dat de punten precies bij de punt van de piramide bij elkaar komen. Bouw je een piramide met als grondvlak een vierkant dan heb je vier precies gelijke driehoeken nodig. De driehoeken zijn dan de zijvlakken van de piramide.

Piramides kun je ook weer maken met allerlei grondvlakken, maar de meest voorkomende zijn het vierkant, zoals de beroemde piramides van Egypte (zie de foto hierboven), en de driehoek met drie even lange zijdes. Deze piramide heet een regelmatig viervlak, maar dat mag je nog even vergeten. Een piramide heeft ook weer hoekpunten en ribben. Het aantal hoekpunten is altijd 1 groter dan het aantal zijden van het grondvlak voor het aantal ribben doe je het aantal zijden van het grondvlak keer twee. Een Egyptische piramide heeft dus 5 hoekpunten en 8 ribben.

Zoals je van een prisma een cilinder kunt maken kun je van een piramide een kegel maken, wanneer het grondvlak rond wordt gemaakt. Het vergt veel geduld om een goede kegel te maken. Je hebt twee cirkels nodig, een gewone en een grotere, waarvan je een groot deel wegknipt. Een voorbeeld van een uitslag van een kegel zie je in het plaatje. En als je het gelukt is heb je een mooie puntmuts gemaakt, of zo’n pion die wegwerkers gebruiken.

Met kubus en balk hadden we ruimtefiguren met zes mogelijke grondvlakken, met prisma en cilinder bleven er nog maar twee over. Bij piramide en kegel is er nog maar één grondvlak en dan vraag je je natuurlijk af of er een ruimtefiguur bestaat zónder grondvlak.

En ja, ook daar heeft de meetkunde in voorzien: dit heet de bol! Geen grondvlak, geen uitslag, geen hoekpunten, geen ribben. Gewoon oppompen en buiten gaan spelen!

De volgende keer ga ik het hebben over lijnen en krommen en een paar van hun bijzonderheden.